the JohnsonSL system in Carnap
Carnap.io is logic software that runs in a browser. JohnsonSL is a propositional logic system for forallx: Mississippi State that can be use in Carnap.
These are the rules of derivation in JohnsonSL:
-
conjunction-introduction (&I): P, Q \(\vdash\) P & Q
-
conjunction-elimination (&E): P & Q \(\vdash\) P or P & Q \(\vdash\) Q
-
disjunction-introduction (\(\vee\)I): P \(\vdash\) P \(\vee\) Q or P \(\vdash\) Q \(\vee\) P
-
disjunction-elimination (\(\vee\)E): P \(\vee\) Q, \(\neg\)P \(\vdash\) Q
-
conditional-elimination (\(\rightarrow\)E): P \(\rightarrow\) Q, P \(\vdash\) Q
-
biconditional-introduction (\(\leftrightarrow\)I): P \(\rightarrow\) Q, Q \(\rightarrow\) P \(\vdash\) P \(\leftrightarrow\) Q
-
biconditional-elimination (\(\leftrightarrow\)E): P \(\leftrightarrow\) Q, P \(\vdash\) Q or P \(\leftrightarrow\) Q, Q \(\vdash\) P
-
double-negation (DN): \(\neg\neg\)P \(\vdash\) P or P \(\vdash\) \(\neg\neg\)P
-
reiteration (R): P \(\vdash\) P
-
conditional-introduction (\(\rightarrow\)I): from a subproof beginning with the assumption A and ending with B, infer A \(\rightarrow\) B.
-
negation-introduction (\(\neg\)I or RAA): from a subproof beginning with the assumption A and ending with B and \(\neg\)B (or \(\neg\)B and B) on consecutive lines, infer \(\neg\)A.
-
negation-elimination (\(\neg\)E or RAA): from a subproof beginning with the assumption \(\neg\)A and ending with B and \(\neg\)B (or \(\neg\)B and B) on consecutive lines, infer A.
The symbols for the logical operators are \(\neg\), &, \(\vee\), \(\rightarrow\), and \(\leftrightarrow\), and they are typed with ~, &, v, ->, and <->. Premises are labeled with ‘PR’. Other assumptions are labeled with ‘AS’. The parentheses dropping conventions are as follows. \(\vee\) binds more strongly than &; & binds more strongly than \(\rightarrow\) and \(\leftrightarrow\); \(\rightarrow\) and \(\leftrightarrow\) bind equally strongly.
Some further details
The disjunction-elimination rule requires the negation, not merely the denial, of one of the disjuncts. Consequently, to derive P from P \(\vee\) \(\neg\)Q and Q, the double-negation rule has to be used—for example, as shown below on the left.
Following Allen and Hand, a reductio ad absurdum rule (RAA) can be used to derive the denial of an assumption. Alternatively, two different rules can be used, a negation-introduction rule and a negation-elimination rule. (Probably, students should only be told about the availability of one or the other.)
The reiteration rule is included to facilitate using RAA or \(\neg\)I/\(\neg\)E with Fitch notation. (Not always, but often, one line of the contradiction will need to be moved down from somewhere else in the proof.)
In the example on the right, the reiteration rule is used to get the contradiction on consecutive lines at the end of the subproof. ‘\(\neg\)I’ in line 6 can be replaced with ‘RAA’ (while keeping everything else the same).
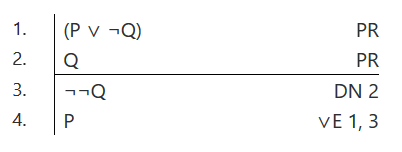
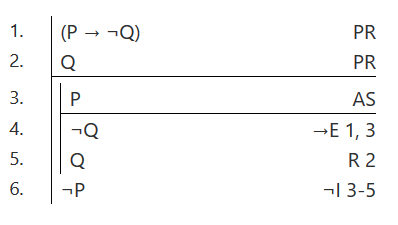
Carnap requires a colon before the PR, AS, or rule. Put the lines numbers being cited after the abbreviation for the rule. For example, as is shown here.
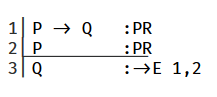
Derived Rules
I don’t use any derived rules in my 1000-level logic course, but the following five are included in JohnsonSLPlus.
-
Hypothetical syllogism (HYP): P \(\rightarrow\) Q, Q \(\rightarrow\) R \(\vdash\) P \(\rightarrow\) R
-
Dilemma (DIL): P \(\vee\) Q, P \(\rightarrow\) R, Q \(\rightarrow\) R \(\vdash\) R
-
Modus tollens (MT): P \(\rightarrow\) Q, \(\neg\)Q \(\vdash\) \(\neg\)P
-
Material conditional (MC): \(\neg\)P \(\vee\) Q \(\dashv\vdash\) P \(\rightarrow\) Q and P v Q \(\dashv\vdash\) \(\neg\)P \(\rightarrow\) Q
-
DeMorgan’s laws (DeM): \(\neg\)(P \(\vee\) Q) \(\dashv\vdash\) \(\neg\)P & \(\neg\)Q and \(\neg\)(P & Q) \(\dashv\vdash\) \(\neg\)P \(\vee\) \(\neg\)Q
Truth Tables
For truth table problems, use system="magnusSL". It will display \(\neg\), &, ∨, \(\rightarrow\), and \(\leftrightarrow\) for the logical operators, and will assign the truth values for the operators in the standard way.
First-order Logic
Although I used to cover first-order logic in my 1000-level logic course, I’ve stopped (and I don’t ever teach any other logic courses). I may go back to including it at some point, but, as it is, I haven’t used Carnap for first-order logic.